ZICONG

梓聪的个人主页

0%

Sklearn机器学习：维度下降和主成分分析

发表于 分类于

简介

这篇文章介绍了降维的基本思路及用奇异值分解（SVD）进行主成分分析（PCA）的操作。

依赖

import numpy as np
from numpy.linalg import svd
import matplotlib
%matplotlib inline
import matplotlib.pyplot as plt
from sklearn.datasets import make_swiss_roll
from sklearn.manifold import LocallyLinearEmbedding
from sklearn.decomposition import PCA

降维的基本思路

投射

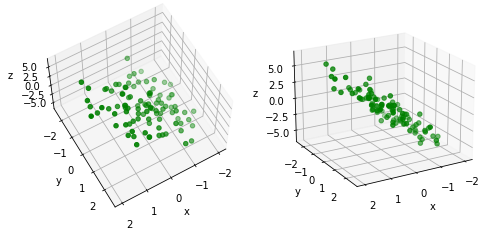
如果数据点不是在各个维度上均匀地分布着：

N = 100
x = np.random.normal(0, 1, N)
y = np.random.normal(0, 1, N)
z = 3 * x + np.random.normal(0, 1, N)

fig = plt.figure(figsize=(8,8))
ax1 = fig.add_subplot(1, 2, 1, projection='3d')
ax1.scatter(x, y, z, c='g', marker='o')
ax1.set_xlabel('x')
ax1.set_ylabel('y')
ax1.set_zlabel('z')
ax1.view_init(60, 60)

ax2 = fig.add_subplot(1, 2, 2, projection='3d')
ax2.scatter(x, y, z, c='g', marker='o')
ax2.set_xlabel('x')
ax2.set_ylabel('y')
ax2.set_zlabel('z')
ax2.view_init(20, 60)

plt.show()

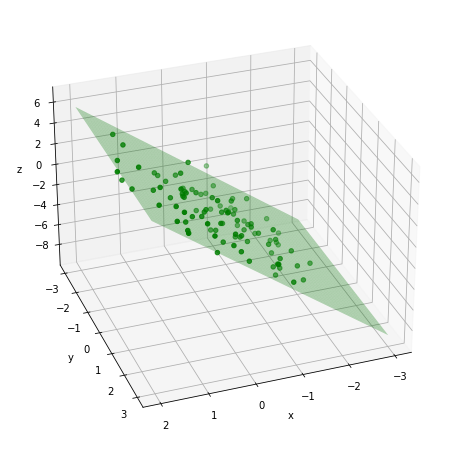
6VKz1H.png

可见，在x和y轴上，数据点比较均匀地分布着。但是在z轴方向上，数据点比较集中在一个平面上面。因此降维的一个方式是找到一个平面，把这些数据点投射在这个平面上，将3维数据简化为2维数据。

fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(1, 1, 1, projection='3d')
ax.scatter(x, y, z, c='g', marker='o')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')

xgrid = np.linspace(-3, 2, 100)
ygrid = np.linspace(-3, 3, 100)
xgrid, ygrid = np.meshgrid(xgrid, ygrid)

ax.plot_surface(xgrid, ygrid, 3 * xgrid, color = 'green', alpha = 0.3)
ax.view_init(30, 70)

6VKx9e.png

流形学习

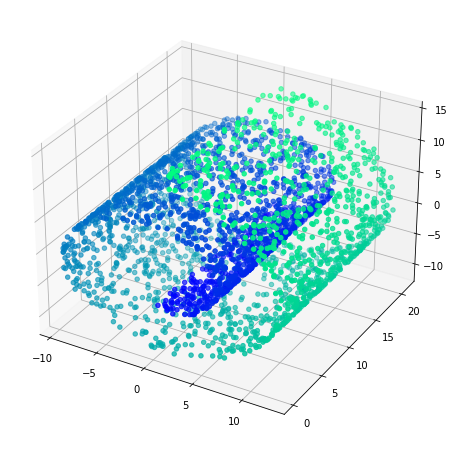
一个$d$维流形可以理解为一个$n$维曲面，其局部可以被$d$维超平面近似。例如，一个在3维空间种的2维流形可以被理解为一个3维曲面，其局部可以被一个2维平面近似。下面的“瑞士卷”是2维流形在3维空间中的例子。

N = 3000
swiss_roll = make_swiss_roll(N)
x, color = swiss_roll

fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x[:,0], x[:,1], x[:,2], c = color, cmap = 'winter')
plt.show()

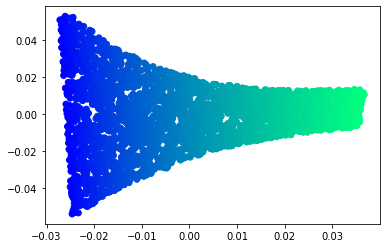
6VKXtO.png

如果可以将这个流形展开，我们可以将3维数据集降维到2维。

embedding = LocallyLinearEmbedding(n_components=2, n_neighbors=12)
x_unfold = embedding.fit_transform(x)

fig, ax = plt.subplots()
ax.scatter(x_unfold[:,0], x_unfold[:, 1], c = color, cmap = 'winter')
plt.show()

6VKOAK.png

主成分分析(PCA)

主成分分析的思路是投影。核心思想是降维后，保留尽量多的数据方差。步骤是：

  1. 确定第一个主成分：找到一个向量，使当数据投影到这个向量上面时，方差最大。
  2. 确定第二个主成分：找到第二个向量与第一个向量正交，使投影到这个向量上的方差最大。

重复这个过程，对于n维数据，最多找到n个主成分。

注意，主成分分解的时候应该先对数据进行转换，使数据集的每个特征的均值为0，主成分向量将默认以0点作为原点。

SVD奇异值分解

设$X$为原数据矩阵，则SVD将其分解为：

$$
\begin{align}
X = U \Sigma V^T
\end{align}
$$

其中，$V$包含了n维矩阵$X$的n个主成分。假设现在要用其中的3个主成分来反映这些数据：

$$
\begin{align}
X_{proj_3} = XW_3
\end{align}
$$

其中，$W_3$包含了$V$的前3列。

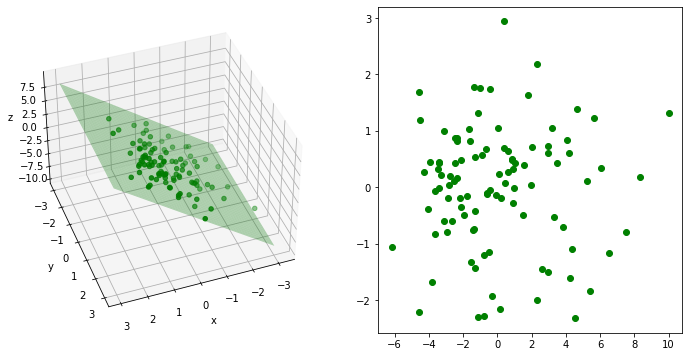
下面用SVD法来分解一个类似第一部分的例子。

N = 100
x1 = np.random.normal(0, 1, N)
x2 = np.random.normal(0, 1, N)
x3 = 3 * x1 + np.random.normal(0, 1, N)
xmat = np.stack((x1, x2, x3), axis=1)
xmat.shape
# 均值归0
xmat_centered = xmat - xmat.mean(axis=0)   # 对每一个特征去均值
u, sigma, v = svd(xmat_centered)

# 投影：取两个主成分
w2 = v.T[:, :2]
xmat_proj = xmat_centered @ w2

# 画图
fig = plt.figure(figsize=(12,6))
ax1 = fig.add_subplot(1, 2, 1, projection='3d')
ax1.scatter(x1, x2, x3, c='g', marker='o')
ax1.set_xlabel('x')
ax1.set_ylabel('y')
ax1.set_zlabel('z')
ax1.view_init(60, 60)

xgrid = np.linspace(-3, 3, 100)
ygrid = np.linspace(-3, 3, 100)
xgrid, ygrid = np.meshgrid(xgrid, ygrid)

ax1.plot_surface(xgrid, ygrid, 3 * xgrid, color = 'green', alpha = 0.3)
ax1.view_init(40, 70)

ax2 = fig.add_subplot(1, 2, 2)
ax2.scatter(xmat_proj[:,0], xmat_proj[:,1], c = 'g')

plt.show()

6VKjhD.png

使用Sklearn包进行SVD

pca = PCA(n_components = 2)
xmat_proj = pca.fit_transform(xmat_centered)

方差解释率（Explained Variance Ratio）

某个主成分的方差解释率，是指此主成分保留的方差占原来的总方差的比例。

evr = pca.explained_variance_ratio_

print(evr)
[0.89202644 0.09989671]

这意味着，第一个主成分保留了89.2%的方差，第二个主成分保留了10.2%的方差。失去的方差是：

print("{: .2%}".format(1 - evr[0] - evr[1]))
 0.81%

选择维度数量

假设要求主成分的方差解释率达到某个值，则在PCA中对n_components中指定一个浮点数。

pca = PCA(n_components=0.95)  # 方差解释率达到95%以上
xmat_proj = pca.fit_transform(xmat_centered)
print("Preserve {:n} dimension(s).".format(xmat_proj.shape[1]))
Preserve 2 dimension(s).

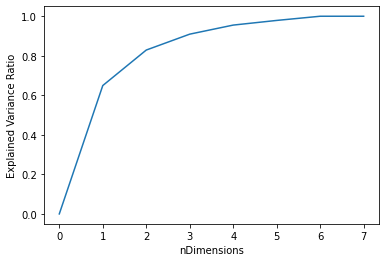
另一方面，我们可以参考维度数量与累计维度解释率的关系。

# 生成示例数据
N = 1000
x1 = np.random.normal(0, 1, N)
x2 = np.random.normal(0, 1, N)
x3 = x1 + x2 * x1 + np.random.normal(0, 1, N)
x4 = x1 + x2**2 + x3 + np.random.normal(0, 1, N)
x5 = x2 + x4 + np.random.normal(0, 1, N)
x6 = x3 + np.random.normal(0, 1, N)
x7 = np.random.normal(0, 1, N)
xmat = np.stack((x1, x2, x3, x4, x5, x6, x7))

# pca
pca = PCA()
pca.fit(xmat)   # 不需要去均值；PCA自动做了
cum_evr = np.cumsum(pca.explained_variance_ratio_)   # 累计方差解释率
cum_evr = np.insert(cum_evr, 0, 0)

# 画图
fig, ax = plt.subplots()
ax.plot(range(0, len(cum_evr)), cum_evr)
ax.set_xlabel('nDimensions')
ax.set_ylabel('Explained Variance Ratio')
plt.show()

6VKq76.png