特点
- 数据驱向型,而非模型驱向型算法
- 不对数据作任何的假设
- 思想:按相似来归类
基本思想
- 对于某个实例$i$,找到与之邻近的实例
- 与之邻近的实例中,归为哪类最多的,该实例就被归为哪一类
- 邻近指的是解释变量值的距离接近
- 距离有很多计算方法,其中基本的一种是使用欧式距离
依赖
import pandas as pd
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.neighbors import NearestNeighbors, KNeighborsClassifier
import matplotlib.pyplot as plt
%matplotlib inline距离公式
- 欧氏距离
- 各个解释变量先进行正态化处理
选择K值
K 值指的是,每个数据找K个最近近邻,这些最近近邻中属于哪类最多的,当前数据就归为哪类。显然,K值应该为奇数。
K值选择的标准是在测试集中应该有最小误差。
- 低K值能反应局部结构,但是同时也引入了噪音
- 高K值减少了噪音,但是无法反映局部结构
当K=N的时候,等同于数据集中所有数据哪类多就归哪类。这是一种naive benchmark
例子:割草机
测试集和训练集
通过收入Income以及房子面积Lot_size来预测实例是否拥有割草机。
mower_df = pd.read_csv('../big_data/datasets/RidingMowers.csv')
mower_df['Number'] = mower_df.index + 1
mower_df.tail()| Income | Lot_Size | Ownership | Number | |
|---|---|---|---|---|
| 19 | 66.0 | 18.4 | Nonowner | 20 |
| 20 | 47.4 | 16.4 | Nonowner | 21 |
| 21 | 33.0 | 18.8 | Nonowner | 22 |
| 22 | 51.0 | 14.0 | Nonowner | 23 |
| 23 | 63.0 | 14.8 | Nonowner | 24 |
将数据分为训练集和测试集。
test_frac = 0.4 # 训练集和测试集比例
train_data, test_data = train_test_split(mower_df, test_size=test_frac)正态化
下面对相应数据进行正态化处理。存在的问题是,我们只知道训练集的均值和方差,(假装)无法得知测试集的均值和方差。因此我们需要先用训练集去“学习”正态化的变换,再用学到的变换引用于全数据集。
# 使用训练集学习变换
scaler = preprocessing.StandardScaler()
scaler.fit(train_data[['Income', 'Lot_Size']])
# 对整个数据集需要变换的数据进行变换
normalized_cols = scaler.transform(mower_df[['Income', 'Lot_Size']])
normalized_cols = pd.DataFrame(normalized_cols, columns = ['zIncome', 'zLot_Size'])
# 重新组装数据集
unchanged_cols = mower_df[['Ownership', 'Number']]
mower_norm = pd.concat([normalized_cols, unchanged_cols], axis=1)
mower_norm.head()| zIncome | zLot_Size | Ownership | Number | |
|---|---|---|---|---|
| 0 | -0.19 | -0.19 | Owner | 1 |
| 1 | 1.08 | -0.87 | Owner | 2 |
| 2 | 0.05 | 1.16 | Owner | 3 |
| 3 | -0.12 | 0.82 | Owner | 4 |
| 4 | 1.16 | 2.01 | Owner | 5 |
下面需要重新提取训练集和测试集。在使用train_test_split()的时候,得到的训练集和测试集将包含一个.index属性。使用该属性将得到一个数组,包含着训练集或测试集中各条数据项在原先总数据集中的索引。利用这点可以在转换后的数据集中提取训练集和测试集。
# 由于行位置不变,使用原先测试集和训练集的索引来提取测试集和训练集
train_norm = mower_norm.iloc[train_data.index]
test_norm = mower_norm.iloc[test_data.index]预测集
生成一个用来预测的数据集。
predict_df = pd.DataFrame([
{'Income': 60, 'Lot_Size': 20},
{'Income': 90, 'Lot_Size': 22},
{'Income': 75, 'Lot_Size': 18}
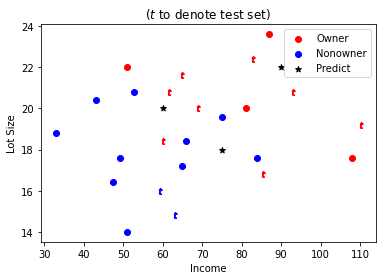
])可视化
fig1, ax = plt.subplots()
# 绘制训练集
subset_owner = train_data[train_data['Ownership'] == 'Owner']
subset_nonowner = train_data[train_data['Ownership'] == 'Nonowner']
ax.scatter(subset_owner['Income'], subset_owner['Lot_Size'], color='r', marker='o', label='Owner')
ax.scatter(subset_nonowner['Income'], subset_nonowner['Lot_Size'], color='b', marker='o', label='Nonowner')
# 绘制测试集
subset_owner = test_data[test_data['Ownership'] == 'Owner']
subset_nonowner = test_data[test_data['Ownership'] == 'Nonowner']
ax.scatter(subset_owner['Income'], subset_owner['Lot_Size'], color='r', marker='$t$')
ax.scatter(subset_nonowner['Income'], subset_nonowner['Lot_Size'], color='b', marker='$t$')
# 绘制预测集
ax.scatter(predict_df['Income'], predict_df['Lot_Size'], color='black', marker='*', label='Predict')
plt.xlabel('Income')
plt.ylabel('Lot Size')
plt.title('($t$ to denote test set)')
plt.legend()
plt.show()求最优K值
求最优K值的方法是找到让测试集accuracy最大化的K。
# 初始化训练集和测试集的x和y
train_norm_x = train_norm[['zIncome', 'zLot_Size']]
train_norm_y = train_norm[['Ownership']]
test_norm_x = test_norm[['zIncome', 'zLot_Size']]
test_norm_y = test_norm[['Ownership']]注意,训练集有14个数据项,因此K的最大取值是15。
train_norm_x.shape(14, 2)
循环K从1到15,训练模型并且获得测试集的accuracy,并把它们存在a list of dict。
# 初始化列表用来存储不同K值获得的测试集的accuracy
results = []
# 循环K
for k in range(1, 15):
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(train_norm_x, train_norm_y.values.ravel())
k_test_accuracy = accuracy_score(test_norm_y, knn.predict(test_norm_x))
results.append({'k':k, 'accuracy': k_test_accuracy})
# 将list of dicts转换为pd.df
results = pd.DataFrame(results)
results| k | accuracy | |
|---|---|---|
| 0 | 1 | 0.5 |
| 1 | 2 | 0.3 |
| 2 | 3 | 0.5 |
| 3 | 4 | 0.3 |
| 4 | 5 | 0.5 |
| 5 | 6 | 0.2 |
| 6 | 7 | 0.2 |
| 7 | 8 | 0.2 |
| 8 | 9 | 0.2 |
| 9 | 10 | 0.2 |
| 10 | 11 | 0.2 |
| 11 | 12 | 0.2 |
| 12 | 13 | 0.2 |
| 13 | 14 | 0.2 |
注意,拟合数据时,y值原本是一列的pd.DataFrame向量,取.values属性获得(14, 1)的np.array向量,再取.ravel()方法获得一个“压扁”的numpy数组。这是该函数所需要传入的。
可以看到,当K取1,3,5时,accuracy最大。取3似最合适。
预测
正态化整个数据集及预测集。
scaler = preprocessing.StandardScaler()
scaler.fit(mower_df[['Income', 'Lot_Size']])
mower_norm_x = scaler.transform(mower_df[['Income', 'Lot_Size']])
mower_norm_y = mower_df[['Ownership']].values.ravel()
predict_norm_x = scaler.transform(predict_df)训练整个数据集:
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(mower_norm_x, mower_norm_y)KNeighborsClassifier(n_neighbors=3)
找到预测集中每个数据项的三个(k=3)最邻近点,返回其距离和索引。
distances, indices = knn.kneighbors(predict_norm_x)
print("Distances: ")
print(distances, "\n")
print("Indices: ")
print(indices)Distances:
[[0.34532669 0.46448259 0.50133206]
[0.40791006 0.52801632 0.69065338]
[0.49402275 0.49402275 0.62479509]]
Indices:
[[ 3 8 13]
[ 7 9 4]
[16 19 14]]
预测:
predictions = knn.predict(predict_norm_x)
for index, prediction in enumerate(predictions):
print(64 * '-')
print(prediction) # 预测值
print(predict_df.iloc[index]) # 第index数据项的取值 (index = 0, 1, 2)
print(mower_df.iloc[indices[index,:]]) # 第index数据项的邻近点的取值
print(mower_norm.iloc[indices[index,:]]) # 正态化的第index数据项的邻近点的取值----------------------------------------------------------------
Owner
Income 60
Lot_Size 20
Name: 0, dtype: int64
Income Lot_Size Ownership Number
3 61.5 20.8 Owner 4
8 69.0 20.0 Owner 9
13 52.8 20.8 Nonowner 14
zIncome zLot_Size Ownership Number
3 -0.12 0.82 Owner 4
8 0.26 0.49 Owner 9
13 -0.55 0.82 Nonowner 14
----------------------------------------------------------------
Owner
Income 90
Lot_Size 22
Name: 1, dtype: int64
Income Lot_Size Ownership Number
7 82.8 22.4 Owner 8
9 93.0 20.8 Owner 10
4 87.0 23.6 Owner 5
zIncome zLot_Size Ownership Number
7 0.95 1.50 Owner 8
9 1.46 0.82 Owner 10
4 1.16 2.01 Owner 5
----------------------------------------------------------------
Nonowner
Income 75
Lot_Size 18
Name: 2, dtype: int64
Income Lot_Size Ownership Number
16 84.0 17.6 Nonowner 17
19 66.0 18.4 Nonowner 20
14 64.8 17.2 Nonowner 15
zIncome zLot_Size Ownership Number
16 1.01 -0.53 Nonowner 17
19 0.11 -0.19 Nonowner 20
14 0.05 -0.70 Nonowner 15
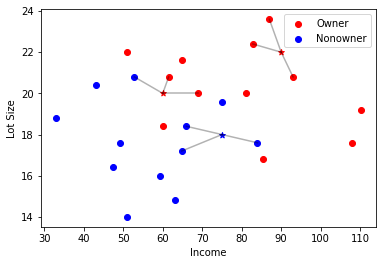
可视化:预测
为了画图,将预测结果(np.array)添加到预测集pd.DataFrame中。
predict_df['Ownership'] = predictions
predict_df| Income | Lot_Size | Ownership | |
|---|---|---|---|
| 0 | 60 | 20 | Owner |
| 1 | 90 | 22 | Owner |
| 2 | 75 | 18 | Nonowner |
fig2, ax = plt.subplots()
# 绘制数据集
subset_owner = mower_df[mower_df['Ownership'] == 'Owner']
subset_nonowner = mower_df[mower_df['Ownership'] == 'Nonowner']
ax.scatter(subset_owner['Income'], subset_owner['Lot_Size'], color='r', label='Owner')
ax.scatter(subset_nonowner['Income'], subset_nonowner['Lot_Size'], color='b', label='Nonowner')
# 绘制预测集
subset_owner = predict_df[predict_df['Ownership'] == 'Owner']
subset_nonowner = predict_df[predict_df['Ownership'] == 'Nonowner']
ax.scatter(subset_owner['Income'], subset_owner['Lot_Size'], color='r', marker='*')
ax.scatter(subset_nonowner['Income'], subset_nonowner['Lot_Size'], color='b', marker='*')
# 绘制近邻点
for i in range(3): # 对预测集每项循环
for j in range(3): # 对邻近点循环
x_values = [mower_df['Income'][indices[i, j]], predict_df['Income'][i]]
y_values = [mower_df['Lot_Size'][indices[i, j]], predict_df['Lot_Size'][i]]
ax.plot(x_values, y_values, color = 'black', alpha = 0.3)
plt.xlabel('Income')
plt.ylabel('Lot Size')
plt.legend()
plt.show()